
https://www.acmicpc.net/problem/11049
행렬 곱셈 최적화 문제는 여러 개의 행렬을 곱할 때 최소한의 연산으로 결과를 구하는 방법을 찾는 거다. 행렬 곱셈은 결합 법칙이 성립하므로, 계산 순서를 바꾸는 방식으로 최적화를 시도할 수 있다. 하지만 순서를 유지한 상태에서 곱셈 순서를 조정해야 하며, 각 연산의 비용은 행렬의 크기에 따라 달라지기 때문에 계산 과정에서 효율적인 방법을 설계해야 한다.
코드에서 핵심은 DP 테이블을 이용해 최소 곱셈 연산 횟수를 저장하며 점진적으로 구간을 확장해 가는 것이다. 예를 들어, 개의 행렬이 있을 때, 각 행렬의 크기를 배열로 저장하고, DP 배열을 통해 특정 구간의 최소 연산 횟수를 반복적으로 계산한다.
input 배열에는 행렬의 크기를 저장합니다. 예를 들어, A(5×3), B(3×2), C(2×6) 라면, input = [5, 3, 2, 6]이된다. dp 배열은 구간별 최소 연산 횟수를 저장하는 테이블로, dp[i][j]는 ii번째부터 jj번째 행렬까지 곱할 때 필요한 최소 연산 횟수를 나타낸다.
행렬 곱셈의 최소 연산 횟수를 구하기 위해 구간을 나누고, 각 구간을 최적화하여 계산합니다. DP 점화식은 다음과 같다:
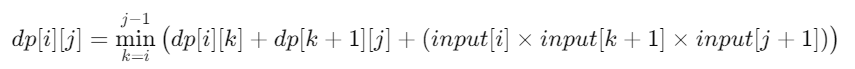
이 식에서 k는 구간을 나누는 기준점이다. dp[i][k]와 dp[k+1][j]는 각각의 부분 구간에서 최소 곱셈 연산 횟수를 나타내며, 두 구간을 곱하는 데 추가로 필요한 연산 횟수는 로 계산된다.
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
static int N;
static int[] input;
static int[][] dp; // [i][j] 는 i부터 j 까지 곱셈중 최소 연산 횟수
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
init();
StringTokenizer st;
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
if (i == 0)
input[0] = Integer.parseInt(st.nextToken());
else
st.nextToken();
input[i + 1] = Integer.parseInt(st.nextToken());
}
for (int i = 2; i < N + 1; i++) {
for (int j = 0; j < N - i + 1; j++) {
dp[j][j + i - 1] = Integer.MAX_VALUE;
for (int k = j; k < j + i - 1; k++) {
int result = dp[j][k] + dp[k + 1][j + i - 1] + (input[j] * input[k + 1] * input[j + i]);
dp[j][j + i - 1] = Math.min(result, dp[j][j + i - 1]);
}
}
}
System.out.println(dp[0][N - 1]);
}
private static void init() {
input = new int[N + 1];
dp = new int[N][N];
}
}'Algorithm & Data Structures > BOJ' 카테고리의 다른 글
| b.2293 동전 1 (0) | 2025.01.21 |
|---|---|
| b2629. 양팔저울 (0) | 2025.01.17 |
| b11066. 파일 합치기 (0) | 2025.01.10 |
| b1300. K번째 수 (0) | 2025.01.08 |
| b6549. 히스토그램에서 가장 큰 직사각형 (0) | 2025.01.06 |